Here you will learn how to use the ratio of the sides of a right triangle, SOHCAHTOA, and right triangle trigonometry to find unknown sides and angles in right angled triangles. You will learn how to label the sides of right-angled triangles and understand what each of the side ratios, sin, cos and tan are, and what their inverses are (\sin^, \cos^, \tan^) in order to problem solve.
Students first learn about right triangle trigonometry in geometry and expand their knowledge as they learn about the unit circle in algebra 2 and precalculus.
SOHCAHTOA is a mnemonic device that gives you an easy way to remember the three main trigonometric ratios of the sides of a right triangle. The trig ratios are used to find the missing sides of the triangle (right triangle) and the missing acute angles.
The names of the three ratios are:
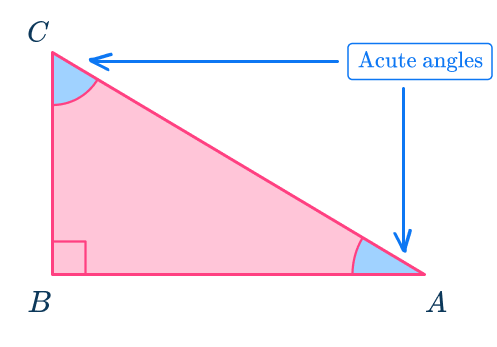
When writing the trigonometric ratios, you must write them with respect to one of the acute angles of the right triangle.
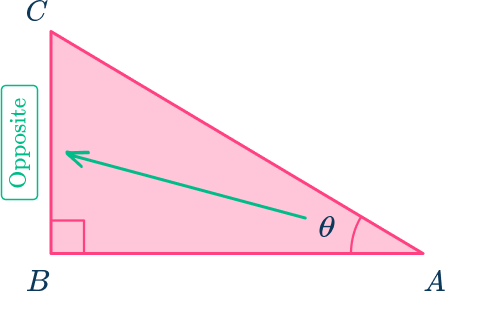
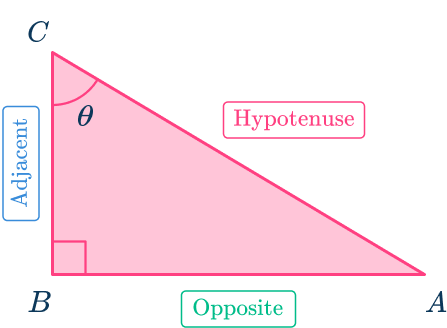
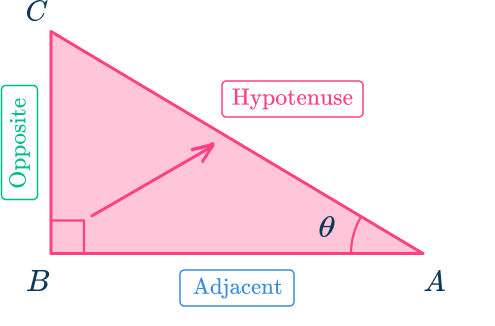
Let’s use angle at A as the acute angle by which to write the 3 main trigonometric ratios. Label this angle \theta. Since all the ratios will be written with respect to angle \theta, the side opposite \theta is called the ‘opposite’ side
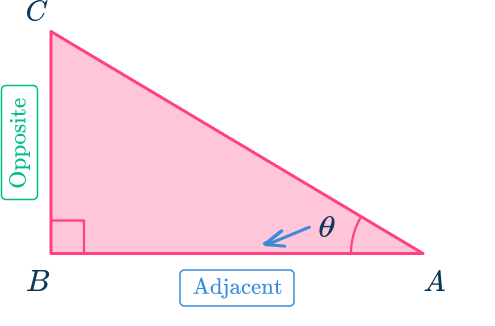
The side that is part of angle \theta or next to angle \theta is called the ‘adjacent’ side.
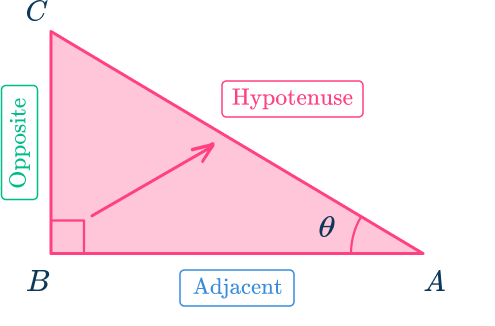
The side across from the right angle is always the ‘hypotenuse’.
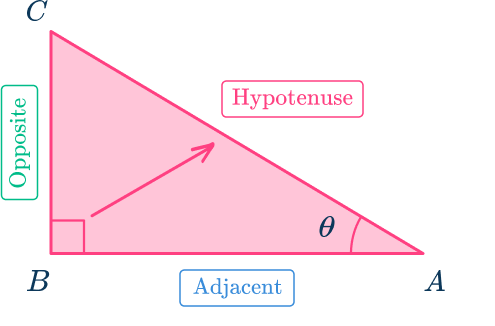
What happens if you use the angle at C instead of the angle at A to write the trigonometric ratios?
Notice how the adjacent side and the opposite side switch since the angle being used is the angle at C, labelled \theta.
![[FREE] Trigonometry Worksheet (Grade 9 to 12)](https://thirdspacelearning.com/wp-content/uploads/2023/07/Trigonometry-check-for-understanding-quiz-listing-image-.png)
Use this quiz to check your grade 9 to 12 students’ understanding of Trigonometry. 15+ questions with answers covering a range of 9th to 12th grade trigonometry topics to identify areas of strength and support!
Use this quiz to check your grade 9 to 12 students’ understanding of Trigonometry. 15+ questions with answers covering a range of 9th to 12th grade trigonometry topics to identify areas of strength and support!
Now that you understand how to label the sides of the right triangle, let’s write the ratios.
You can also remember the abbreviation for SOHCAHTOA using triangles.
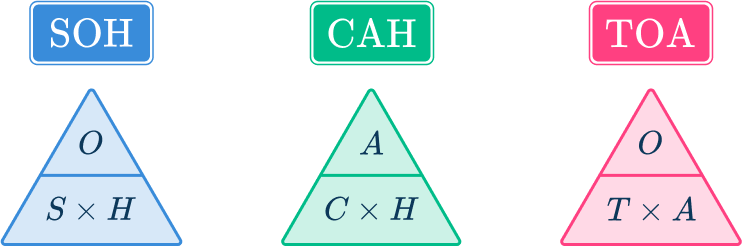
Sine, Cosine and Tangent are therefore trigonometric functions as the sine, cosine, or tangent of an angle \theta is equal to the division of the two respective sides O\div, A\div or O\div.
Each SOHCAHTOA triangle can be used to determine the missing side, or missing angle of a right-angled triangle. Cover up the letter you want to find and calculate the product or division of the other two letters using one of the three formulae highlighted in the table.
How does this relate to high school math?
In order to use SOHCAHTOA to find the missing side length of a right triangle:
Calculate the side of the right triangle labeled x.
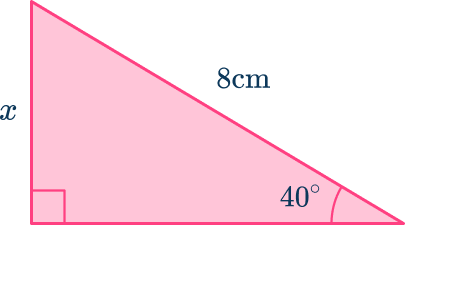
Using the 40^ angle, the side marked x is the opposite side and the side marked 8\mathrm is the length of the hypotenuse because it is across from the right angle.
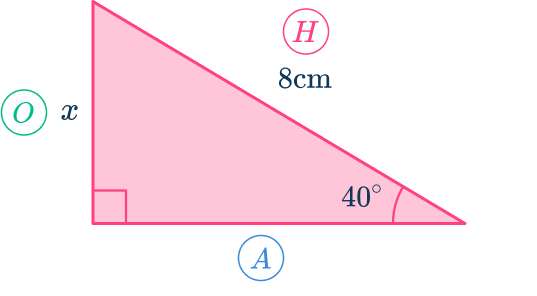
2 Determine the trigonometric ratio to use and write the formula with the correct subject.
The hypotenuse (H) is known, and the opposite side (O) is what you want to find.
The adjacent side (A) is unknown and so not useful for this problem.
Looking at SOHCAHTOA, the sine function (S) is the ratio of the opposite side (O) and the hypotenuse (H).
You therefore use the sine function:
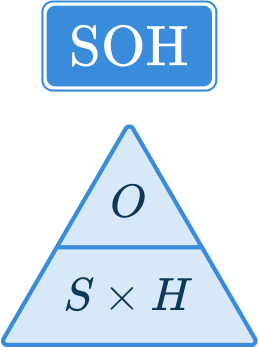
Using the formula triangle, cover up the opposite side (O) as you want to calculate this length. This gives the formula:
3 Substitute known values into the formula to find the missing side.
As the opposite side O=x\mathrm, the hypotenuse H=8\mathrm, and \theta=40^,
4 Calculate the unknown side.
Use your calculator to find the solution
Always check that the answer is reasonable:
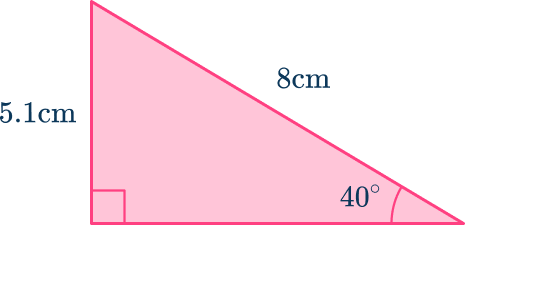
As 5.14\mathrm is shorter than the length of the hypotenuse (8\mathrm), the answer is reasonable.
Calculate the side of the right triangle labeled x.
Label the sides of the right triangle with respect to one of the acute angles.
Using the angle labeled 36^, the side marked x is the adjacent side (A) because it is next to the angle and the side marked as 15\mathrm is the hypotenuse (H) because it is across from the right angle.
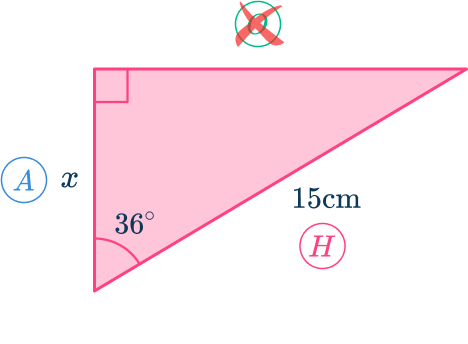
Determine the trigonometric ratio to use and write the formula with the correct subject.
The hypotenuse (H) is known, and the adjacent side (A) is what you want to find.
The opposite side (O) is unknown and so not useful for this problem.
Looking at SOHCAHTOA, the cosine function (C) is the ratio of the adjacent side (A) and the hypotenuse (H).
You therefore use the cosine function:
Using the formula triangle, cover up the adjacent side (A) as you want to calculate this length. This gives the formula:
Substitute known values into the trig ratio to find the missing side.
As the adjacent side A=x\mathrm, the hypotenuse H=15\mathrm, and \theta=36^,
Calculate the unknown side.
Use your calculator to find the solution
Always check that the answer is reasonable:
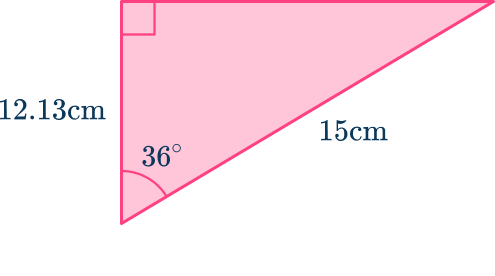
The value of the side being 12.13\mathrm makes sense with the sketched out triangle
Calculate the side labeled x .
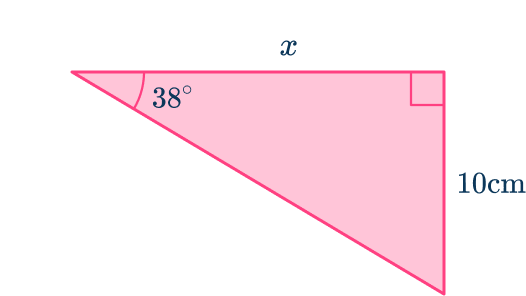
Label the sides of the right triangle with respect to one of the acute angles.
Using the angle marked 38^ , the side marked as x is the adjacent side because it is next to the angle, and the side marked as 10\mathrm is the opposite side because it is opposite the angle.
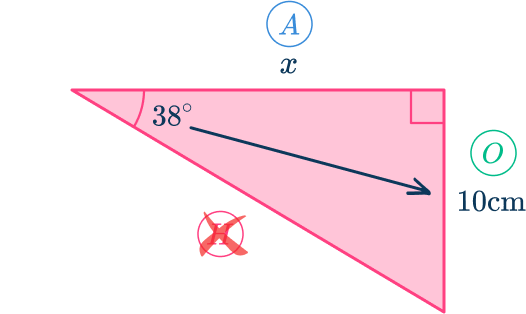
Determine the trigonometric ratio to use and write the formula with the correct subject.
The opposite side (O) is known, and the adjacent side (A) is what you want to find.
The hypotenuse (H) is unknown and so not useful for this problem.
Looking at SOHCAHTOA, the tangent function (T) is the ratio of the opposite side (O) and the adjacent side (A).
You therefore use the tangent function:
Using the formula triangle, cover up the adjacent side (A) as you want to calculate this length. This gives the formula:
Substitute known values into the trig ratio to find the missing side.
As the opposite side O=10\mathrm, the adjacent side A=x\mathrm, and \theta=38^,
Calculate the unknown side.
Use your calculator to find the solution
Always check that the answer is reasonable:
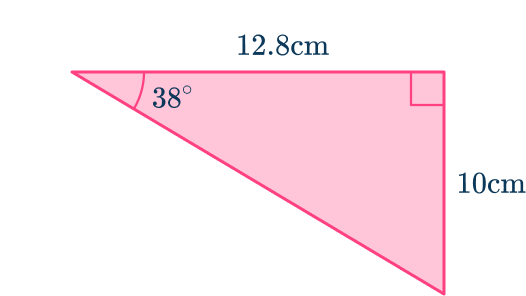
The longer side is opposite the larger angle. As the sum of angles in a triangle is 180^, the other angle in the triangle is 52^. The longer side is opposite the larger angle so this solution is reasonable.
In order to find missing angles using SOHCAHTOA:
Calculate the angle labeled \theta.
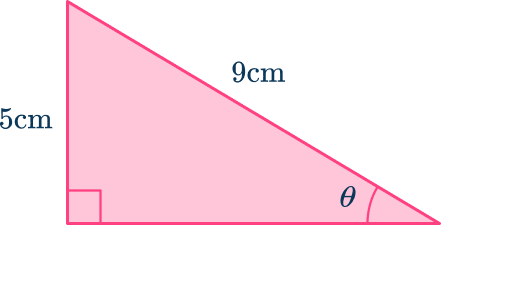
Label the sides of the right triangle with respect to one of the acute angles.
The side marked as 5\mathrm is opposite the angle, so this is the opposite side.
The side marked as 9\mathrm is the hypotenuse because it is across from the right angle.
SOHCAHTOA 26 US" width="573" height="296" />
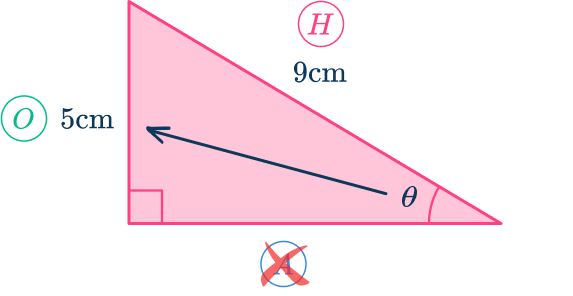
Determine the trigonometric ratio to use and write the inverse trig formula with \bf as the subject.
Looking at SOHCAHTOA, the sine function (S) is the ratio of the opposite side (O) and the hypotenuse (H).
As you are finding the angle, use the inverse sine function:
Note, you can use the formula for the sine function (\sin(\theta)=\cfrac), but you will need to rearrange it by finding the inverse sine of each side to obtain \theta=\sin^\left(\cfrac\right).
Substitute the two known side lengths into the formula.
As the opposite side O=5\mathrm and the hypotenuse H=9\mathrm,
Calculate the unknown angle.
\theta=\sin^\left(\cfrac\right)=33.75^\textRemember we can get \sin^( on the calculator by pressing SHIFT or 2 nd and then sin. Don’t forget to close the bracket as well.
Always check that the answer is sensible:
You can estimate from the sketch that \theta is an acute angle.
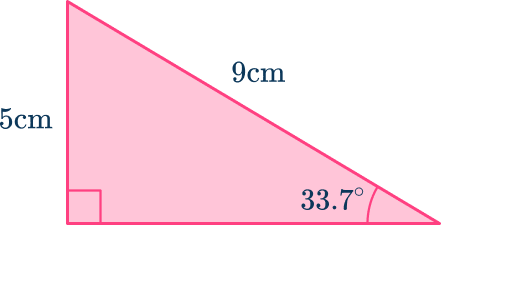
As 33.7^ is less than 90^, the answer is reasonable.
Calculate the angle labeled \theta .
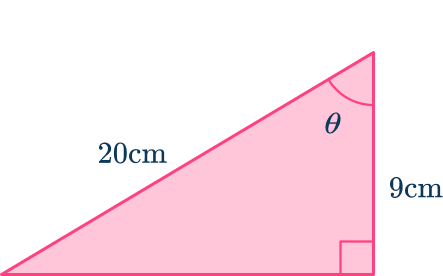
Label the sides of the right triangle with respect to one of the acute angles.
The side marked as 9\mathrm is next to the angle, so this is the adjacent side.
The side marked as 20\mathrm is the hypotenuse because it is across from the right angle.
Determine the trigonometric ratio to use and write the inverse trig formula with \bf as the subject.
Looking at SOHCAHTOA, the cosine function (C) is the ratio of the adjacent side (A) and the hypotenuse (H).
As you are finding the angle, use the inverse cosine function:
Substitute the two known side lengths into the formula.
As the adjacent side A=9\mathrm and the hypotenuse H=20\mathrm,
Calculate the unknown angle.
\theta=\cos^\left(\cfrac\right)=63.26^\textRemember we can get \cos^( on the calculator by pressing SHIFT or 2 nd and then cos. Don’t forget to close the bracket as well.
Always check that the answer is sensible:
You can estimate from the sketch that \theta is an acute angle.
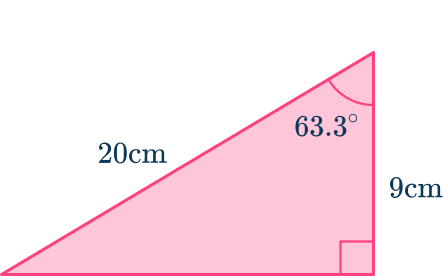
As 63.3^ is less than 90^, the answer is reasonable.
Calculate the angle labeled \theta .
Label the sides of the right triangle with respect to one of the acute angles.
The side marked as 15\mathrm is opposite the angle \theta , so this is the opposite side.
The side marked as 7\mathrm is the adjacent side because it is next to the angle.
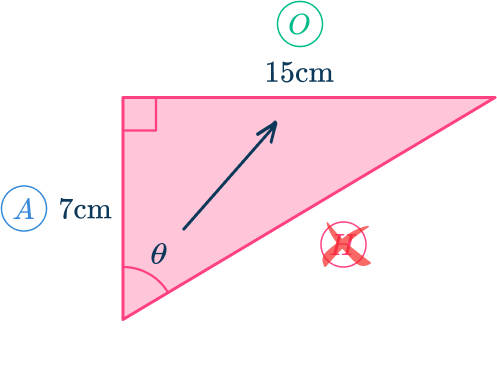
Determine the trigonometric ratio to use and write the inverse trig formula with \bf as the subject.
Looking at SOHCAHTOA, the tangent function (T) is the ratio of the opposite side (O) and the adjacent side (A).
As you are finding the angle, use the inverse tangent function:
Substitute the two known side lengths into the formula.
As the opposite side O=15\mathrm and the adjacent side A=7\mathrm,
Calculate the unknown angle.
\theta=\tan^\left(\cfrac\right)=64.98^\textRemember we can get \tan^( on the calculator by pressing SHIFT or 2 nd and then tan. Don’t forget to close the bracket as well.
Always check that the answer is sensible:
Draw an accurate sketch of the triangle and measure the angle using a protractor.
For example, if trying to calculate the adjacent side:
\tan(90)=\cfrac> \rightarrow This is an incorrect ratio.
You cannot use the 90^ angle when writing the ratio and 24 is NOT the opposite side.
The hypotenuse is always the side across from the right angle and the longest side.
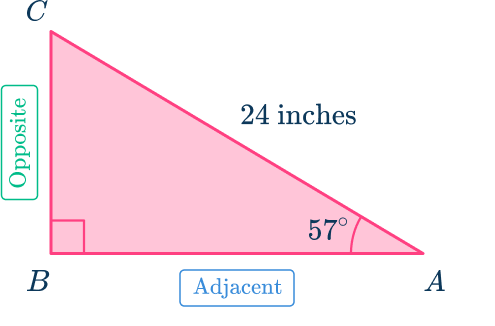
1. Calculate the length of the side labeled x. Round your answer to the nearest tenth.
